
CALCULO INTEGRAL
APLICACIONES DE LA INTEGRAL
UNA DE LAS APLICACIONES DEL CALCULO INTEGRAL SE DA EN EL ÁREA DE LA ECONOMÍA AL CONOCER LA "CURVA COSTO BENEFICIO" UNA HERRAMIENTA MUY ÚTIL PARA EMPRESAS EN EL DESARROLLO Y CONOCER LOS NIVELES DE DEMANDA

Un análisis de costo beneficio es un estudio del retorno, no sólo financiero de nuestras inversiones, sino también de aspectos sociales y medioambientales de lo que el proyecto tiene alguna o toda influencia.
El análisis de datos está en todo su esplendor. Vivimos en la era de la analítica, gran parte de nuestras decisiones están basadas según los resultados que obtenemos a diario. Posibles escenarios, estudios de mercado, planes de negocios, gráficas de resultados. Cada vez disponemos de más razones y recursos con los que conseguir una efectiva cuantificación de consecuencias sociales y económicas de nuestro trabajo.
Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee : integral de f de x diferencial de x.
∫ es el signo de integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C

INTEGRAL INDEFINIDA, USADA EN VARIOS CAMPOS LABORALES O ACADEMICOS
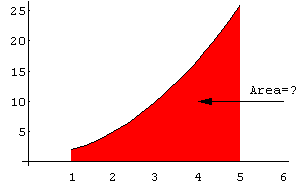
AREA BAJO LA CURVA es el primer paso para desarrollar el concepto de integral. El área bajo la curva formada por el trazo de la función f(x) y el eje x se puede obtener aproximadamente, dibujando rectángulos de anchura finita y altura f igual al valor de la función en el centro del intervalo.

Se denomina SOLIDO DE REVOLUCION o volumen derevolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo, las cuales pueden o no cruzarse. Dicha recta se denomina eje de revolución. Sea f una función continua y positiva en el intervalo [a,b].